The Big Four Quantum Algorithms
These are my highly simplified single-line interpretations of the big-4 algorithns or the problems they are solving in Quantum Computing. I know, this won't do justice to the full story of the great algorithms, but I'm trying to see how the great minds have progressed through these ideas and how they are related to each other, if at all.
Deutsch-Jozsa
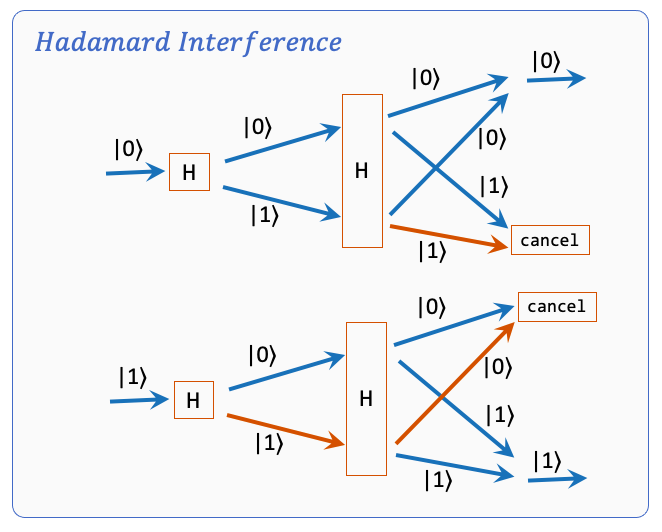
Half of the states have changed or none of them changed. Do we know which case happened? Apply Hadamard.
Shor
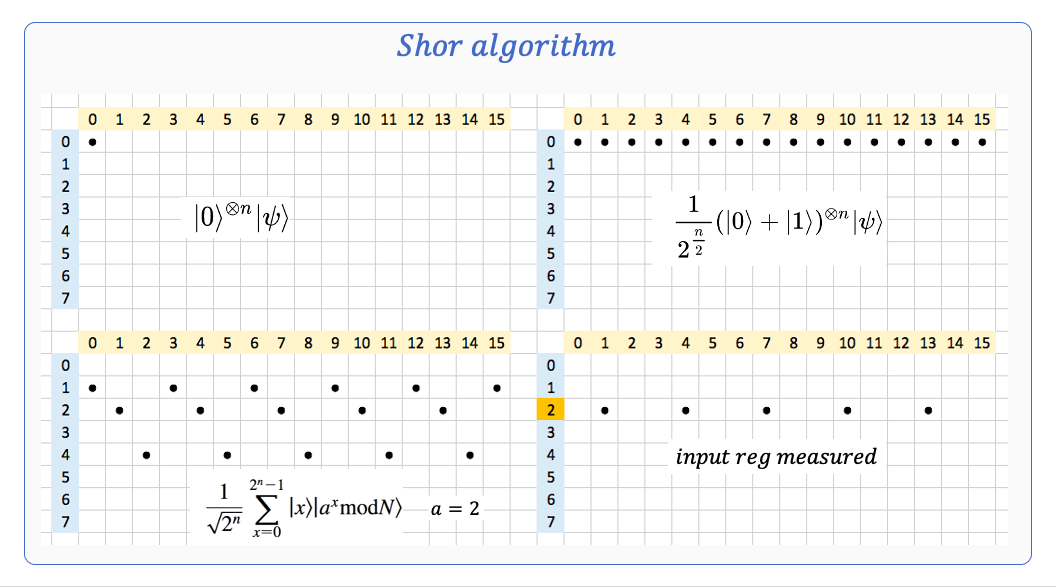
Every Nth state has changed. Do we know N? Apply QFT.
Shor's idea is to exploit the wave-like pattern in modular exponentiation (due to Euler's totient fucntion). The quantum states are superimposed and collapsed gradually to reveal the wave-length (period-finding), which is the solution to solving the integer factoring problem in polynomial time.
Grover
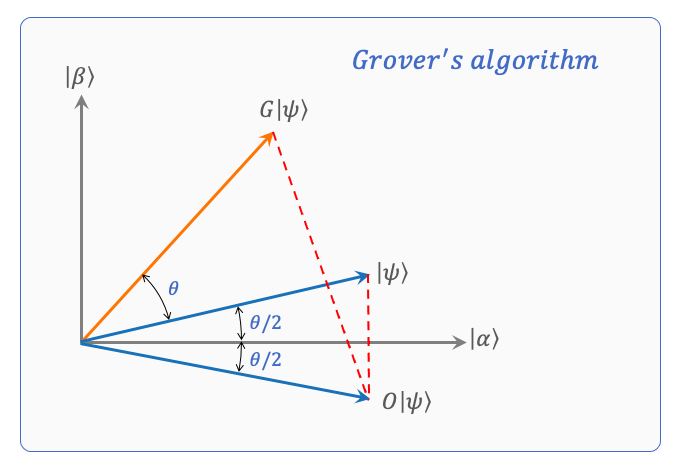
One state has changed. Do we know which one? Amplify amplitude.
Grover's algorithm is typically described as a search algorithm for an unsorted database having N records in O(√N) time. For classical algorithms, this search would take O(N) in time (linear search) for the worst case.
Another way to look at the algorithm would be as "function inverter". That is, Grover's algorithm can help us calculate x, given y for a function y=f(x).
Counting by phase estimation
Multiple states have changed. Do we know how many? Estimate phase.
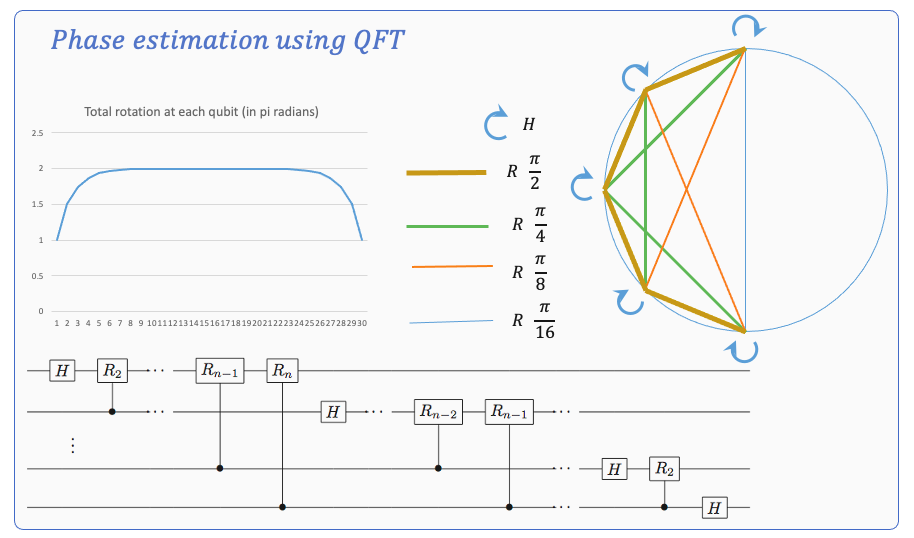
Other areas which I think can be explored further -
- Multiple states have changed. Do we know which ones?
- States have a repeating pattern. Can we extract it?
- Assume that you have a massive quantum parallelism available for processing. How do you change classical programs?