The Great Dot Product

It is hard to imagine a mathematical area not influenced by dot product. ML uses dot product heavily in the core of its algorithms. I wanted to explore into geometrical meaning of dot product, beyond the usual explanation of product of a magnitude of a vector with the projection of of another. This doesn't dound very symmetrical or geometrical. Also in this form, it sounds quite different from its cousing cross product.

Cross Product of two vectors can be thought of as an area spanned by the two vectors. Very intuitive. So how does a dot product look like? I have created some Geogebra notebooks below, to explore.

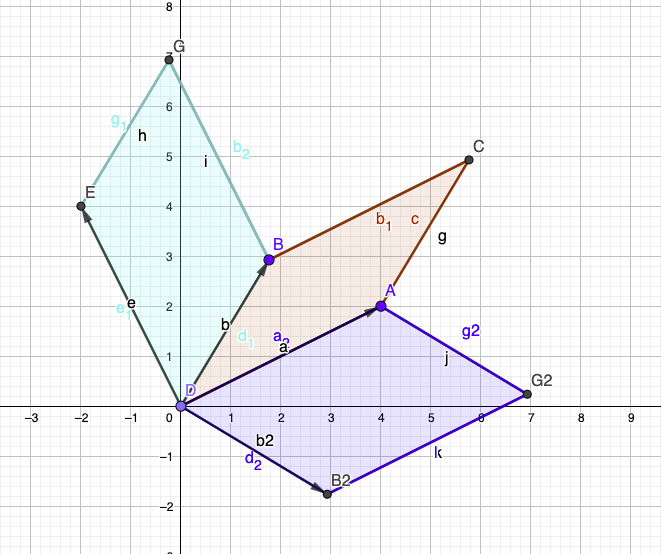
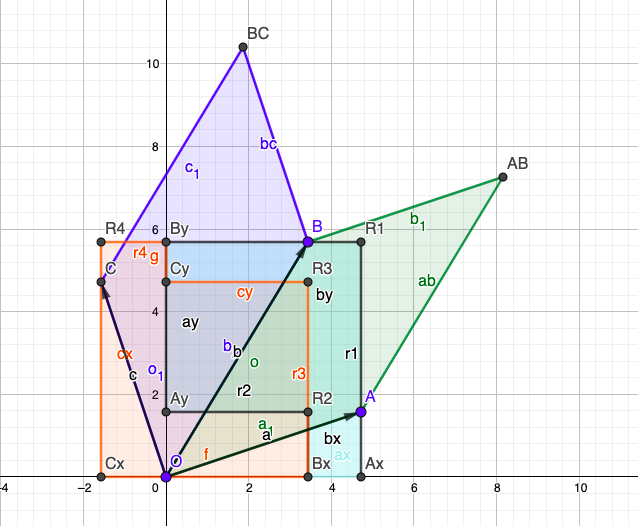
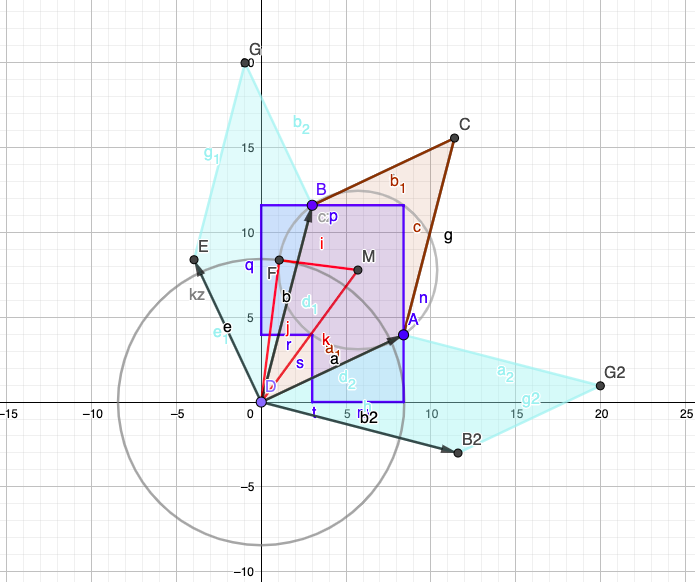
Interesting. The Cross Product is flanked by the Dot Product on both sides. There is a lot going on in the last diagram with circles entering into the picture. The circles are orthogonal.